Everything of Study : November 2013

Sabtu, 30 November 2013

Teorema pytagoras

Sobat pasti tidak asing lagi dengan rumus a² + b²= c². Itu adalah rumus dari teorema pythagoras. Kurang lebih 2500 tahun yang lalu seorang filsuf yunani bernama Pythagoras menemukan fakta menarik tentang segitiga. Beliau menyatakan dalam sebuah segitiga siku-siku (salah satu sudutnya 90o), kuadrat sisi miringnya akan sama dengan jumlah kuadrat dari 2 sisi yang lain. Mari sobat hitung simak gambar berikut.

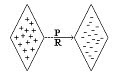
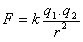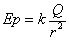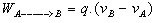Jika kita punya sebuah segitiga siku-siku dengan sisi a,b, dan c

Akan berlaku

a² + b² = c²

dalam teorema yang dikemukakan oleh Pythagoras, sisi c atau sisi miring disebut dengan hipotenusa

Jika kuadrat merupakan luasan persegi, maka berlaku luasan persegi dari panjang sisi a + luasan persegi dari panjang sisi b = luasan panjang dari sisi c. Luasan ini akan kita gunakan untuk membuktikan rumus teorema Pythagoras, simak gambar berikut

dengan melihat gambar di atas maka

Pembuktian Toerema Pythagoras
Banyak cara yang bisa digunakan untuk membuktikan kebenaran teorema ini. Sobat bisa praktek langsung dengan alat atau menggunakan coret-coretan di kertas. Berikut ini pembuktian paling sederhana tentang kebenaran teorema Pythagoras dengan menggunakan luasan segitiga dan luasan persegi. Jika sobat punya segitiga siku-siku, cobalah menyusunnya membentuk kotak seperti di bawah ini.

Luas Persegi Besar = Luas Persegi
putih Kecil + Luas 4 Segitiga
(a+b)²= c²+ 2.a.b
a²+ 2ab + b²= c²+ 2ab

a²+b²= c²

Pembuktian teorema Pythagoras lainnya yang bisa sobat lakukan adalah menggunakan tegel lantai, jika lantai rumah ada tegel atau ubinya, coba sobat buat segitiga alas 4 ubin dan tinggi 4 ubin

Coba sobat ukur panjang sisi miring dari segitiga di ubin tersebut (garis warna merah). Jika pengukuran sobat benar maka akan di dapat panjang sisi miring adalah 5 kali panjang ubin.

FAKTORISASI SUKU ALJABAR

RINGKASAN MATERI

A. Pengertian Faktorisasi

Faktorisasi aljabar adalah mengubah penjumlahan aljabar menjadi perkalian faktor-faktornya.

Contoh :

Karena 8 = 1 x 8, atau 8 = 2 x 4, maka 1, 2, 4 dan 8 adalah faktor-faktor dari 8

B. Bentuk Distributif

ab + ac = a(b + c)

ab – ac = a(b – c), dengan a adalah faktor suku aljabar yang sama.

Contoh :

15p² + 9p = 3p(5p + 3)

C. Bentuk Selisih Dua Kuadrat

a² – b² = (a + b)(a – b)

Contoh :

16m² – 9 = (4m + 3)(4m – 3)

D. Bentuk Kuadrat Sempurna

a² + 2ab + b² = (a + b)²

a² – 2ab + b² = (a – b)²

Contoh :

x² + 10x + 25 = (x + 5)²

x² – 16x + 64 = (x – 8)²

E. Bentuk ax² + bx +c, dengan a = 1

x² + bx + c = (x + p)(x + q)

dengan syarat : pq = c dan p + q = b

Contoh :

x² + 8x + 12 =(x + 2)(x + 6)

F. Bentuk ax² + bx +c, dengan a ≠ 1

dengan syarat : pq = ac dan p + q = b

G. Menyederhanakan Pecahan Aljabar

Contoh :

Cara : Bentuk aljabar difaktorkan dan faktor yang sama di hilangkan

Rumus rumus Getaran Dan Gelombang

Rumus Periode dan Frekuensi Getaran

Periode Getaran

T = t/n

Dengan ketentuan:

T = Periode (sekon)
t = Waktu (sekon)
n = Jumlah getaran

Frekuensi Getaran

f = n/t

Dengan ketentuan:

f = Feminim (Hz)
n = Jumlah getaran
t = Waktu (sekon)

Hubungan antara Periode dan Frekuensi Getaran

Terdapat 2 rumus, yaitu:

T = 1/f
f = 1/t

Dengan ketentuan:

T = Periode (sekon)
f = Frekuensi (Hz)

Getaran Dan Gelombang

GETARAN DAN GELOMBANG

1. Getaran

Getaran didefinisikan sebagai gerak bolak-balik secara berkala melalui titik seimbangnya. Dalam getaran terdapat dua besaran yaitu:

a. Amplitudo

Amplitudo adalah simpangan paling besar, sedangkan simpangan didefinisikan sebagai jarak benda dari titik seimbangnya.
Untuk melihat rumusnya klik disini

b. Periode dan frekuensi

Periode (T) adalah selang waktu yang diperlukan untuk menempuh satu getaran; satuannya dalam SI adalah sekon (disingkat s). Frekuensi (f) adalah banyaknya getaran yang dilakukan dalam satu sekon; satuannya dalam SI adalah hertz (disingkat Hz).

Untuk melihat rumusnya klik disini

2. Gelombang

a. Pengertian dan Sifat Umum Gelombang

Gelombang adalah suatu usikan (getaran) yang merambat, yang membawa energi dari satu tempat ke tempat yang lain. Sewaktu gelombang merambat, mediumnya tidak ikut merambat. Sedangkan energi gelombang berasal dari getaran. Sedang medium didefinisikan sebagai zat atau bahan dimana getaran merambat. Contoh, medium dari gelombang laut adalah air laut dan medium dari gelombang bunyi adalah udara.

Berdasarkan perlu atau tidaknya medium, gelombang di bagi menjadi dua yaitu gelombang mekanik dan gelombang elektromagnetik.

Gelombang mekanik, seperti gelombang laut, gelombang tali, dan gelombang bunyi memerlukan medium untuk merambat. Jadi gelombang mekanik adalah gelombang yang perambatan getarannya memerlukan medium.
Gelombang elektomagnetik, getaran dari gelombang elektromagnetik dapat merambat melalui ruang hampa (ruang tanpa pertikel), sehingga gelombang elektromagnetik dapat hadir baik ada medium atau tidak. Seperti cahaya matahari yang termasuk gelombang elektromagnetik mermbat melalui ruang hampa yang terdapat dalam atmosfer untuk dapat sampai kepermukaan bumi.

Kemudian berdasarkan acuan arah rambat gelombang terhadap arah getarnya, gelombang dibagi menjadi dua, yaitu gelombang tranversal dan gelombang longitudinal.

Gelombang tranversal adalah gelombang yang arah rambatnya tegak lurus dengan arah getarnya. Rambatan gelombang tranversal berbentuk bukit dan lembah sehingga hanya dapat terjadi dalam zat padat atau vakum.
Gelombang longitudinal adalah gelombang yang arah rambatnya sejajar dengan arah getarannya. Rambatan gelombang longitudinal berbentuk rapatan dan regangan, sehingga dapat terjadi dalam padatan, cairan, dan gas.

b. Istilah-istilah dalam Gelombang

Isitilah-istilah dalam gelombang adalah periode dan frekuensi gelombang, satu gelombang, panjang gelombang dan amplitudo; secara lebih jelasnya diuraikan sebagai berikut:

1. Periode dan frekuensi gelombang

Periode gelombang (T) adalah waktu yang diperlukan untuk melakukan satu gelombang melalui satu titik yang dinyatakan dalam satuan sekon (disingkat s). Sedangkan frekuensi gelombang (f) adalah jumlah gelombang yang lewat dalam setiap sekon yang dinyatakan dalam satuan hertz (disingkat Hz). Hubungan antara periode dan frekuensi gelombang dituliskan sebagai berikut:
Untuk melihat rumusnya klik disini

2. Satu Gelombang

a. Gelombang tranversal

Pada gelombang tranversal, satu gelombang terdiri dari satu bukit dan satu lembah, seperti yang terlihat pada gambar berikut:

Gambar 2.3

Gelombang tranversal

Keterangan:

1 bukit = a – b – c atau e – f – g

1 lembah = c – d – e

1 gelombang = a – b – c – d – e

Amplitido = simpangan terjauh = b – b’ atau d’ – d atau f – f’

Untuk melihat rumusnya klik disini

b. Gelombang Longitudinal

Pada gelombang longitudinal, satu gelombang terdiri dari satu rapatan dan satu renggangan, seperti yang terlihat pada gambar berikut:

Gambar 2.4

Gelombang longitudinal

Keterangan:

1 gelombang = 1 rapatan + 1 renggangan atau

1 gelombang = rapatan – rapatan; atau renggangan – renggangan

Untuk melihat rumusnya klik disini

3. Panjang gelombang

Panjang gelombang (λ) adalah jarak antara dua puncak (rapatan) gelombang yang berdekatan atau jarak antara dua dasar (renggangan) gelombang yang berdekatan. Dalam SI, satuan panjang gelombang adalah meter (disingkat m).

4. Cepat rambat gelombang

Cepat rambat gelombang (v) adalah jarak yang ditempuh gelombang dalam selang waktu tertentu. Dalam SI, satuan cepat rambat gelombang adalah m/s. Rumus dasar gelombang adalah:

atau v = λ x f

Keterangan:

v = cepat rambat gelombang (m/s)

λ = panjang gelombang (m)

T = periode (s)

f = frekuensi (Hz)

5. Pemantulan gelombang

Pemantulan gelombang pada ujung tetap akan memgalami perubahan bentuk atau fase. Tetapi, pemantulan gelombang pada ujung bebas tidak mengubah bentuk atau fasenya.
Untuk melihat rumusnya klik disini

Barisan Dan Deret

BARISAN ARITMATIKA

U₁, U₂, U₃, .......U_n-1, U_n disebut barisan aritmatika, jika
U₂- U₁ = U₃- U₂ = .... = U_n - U_n-1 = konstanta

Selisih ini disebut juga beda (b) = b =U_n - U_n-1

Suku ke-n barisan aritmatika a, a+b, a+2b, ......... , a+(n-1)b
U₁, U₂, U₃ ............., U_n

Rumus Suku ke-n :

U_n = a + (n-1)b = bn + (a-b) ® Fungsi linier dalam n

DERET ARITMATIKA

a + (a+b) + (a+2b) + . . . . . . + (a + (n-1) b) disebut deret aritmatika.

a = suku awal
b = beda
n = banyak suku
U_n = a + (n - 1) b adalah suku ke-n

Jumlah n suku

Sn = 1/2 n(a+U_n)
= 1/2 n[2a+(n-1)b]
= 1/2bn² + (a - 1/2b)n ® Fungsi kuadrat (dalam n)

Keterangan:

Beda antara dua suku yang berurutan adalah tetap (b = S_n")
Barisan aritmatika akan naik jika b > 0
Barisan aritmatika akan turun jika b < 0
Berlaku hubungan U_n = S_n - S_n-1 atau Un = S_n' - 1/2 S_n"
Jika banyaknya suku ganjil, maka suku tengah

U_t = 1/2 (U₁ + U_n) = 1/2 (U₂ + U_n-1) dst.
S_n = 1/2 n(a+ U_n) = nU_t ® U_t = Sn / n
Jika tiga bilangan membentuk suatu barisan aritmatika, maka untuk memudahkan perhitungan misalkan bilangan-bilangan itu adalah a - b , a , a + b

BARISAN GEOMETRI

U₁, U₂, U₃, ......., U_n-1, U_n disebut barisan geometri, jika

U₁/U₂ = U₃/U₂ = .... = U_n / U_n-1 = konstanta

Konstanta ini disebut pembanding / rasio (r)

Rasio r = U_n / U_n-1

Suku ke-n barisan geometri

a, ar, ar² , .......ar^{^n-1}
U₁, U₂, U₃,......,U_n

Suku ke n U_n = ar^{^n-1} ® fungsi eksponen (dalam n)

DERET GEOMETRI

a + ar² + ....... + ar^n-1 disebut deret geometri
a = suku awal
r = rasio
n = banyak suku

Jumlah n suku

Sn = a(r^ⁿ-1)/r-1 , jika r>1
= a(1-r^ⁿ)/1-r , jika r<1 ® Fungsi eksponen (dalam n)

Keterangan:

Rasio antara dua suku yang berurutan adalah tetap
Barisan geometri akan naik, jika untuk setiap n berlaku
U_n> U_n-1
Barisan geometri akan turun, jika untuk setiap n berlaku
U_n < U_n-1

Bergantian naik turun, jika r < 0
Berlaku hubungan U_n = S_n - S_n-1
Jika banyaknya suku ganjil, maka suku tengah
_______ __________
Ut = Ö U₁xU_n = Ö U₂ X U_n-1 dst.
Jika tiga bilangan membentuk suatu barisan geometri, maka untuk memudahkan perhitungan, misalkan bilangan-bilangan itu adalah a/r, a, ar

DERET GEOMETRI TAK BERHINGGA

Deret Geometri tak berhingga adalah penjumlahan dari

U₁ + U₂ + U₃ + ..............................

¥
å Un = a + ar + ar² .........................
n=1

dimana n ® ¥ dan -1 < r < 1 sehingga rⁿ ® 0

Dengan menggunakan rumus jumlah deret geometri didapat :

Jumlah tak berhingga    S_{_¥} = a/(1-r)

Deret geometri tak berhingga akan konvergen (mempunyai jumlah) untuk -1 < r < 1

Catatan:

a + ar + ar²+ ar³+ ar⁴+ .................

Jumlah suku-suku pada kedudukan ganjil

a+ar²+ar⁴+ .......                     S_ganjil = a / (1-r²)

Jumlah suku-suku pada kedudukan genap

a + ar³ + ar⁵ + ......                  S_genap = ar / 1 -r²

Didapat hubungan : S_genap / S_ganjil = r

PENGGUNAAN
Perhitungan BUNGA TUNGGAL (Bunga dihitung berdasarkan modal awal)
M₀, M₁, M₂, ............., M_n
M₁ = M₀ + P/100 (1) M₀ = {1+P/100(1)}M₀
M₂ = M₀ + P/100 (2) M₀ = {1+P/100(2)} M₀
.
.
.
.
M_n =M₀ + P/100 (n) M₀ ® M_ⁿ = {1 + P/100 (n) } M₀

Perhitungan BUNGA MAJEMUK (Bunga dihitung berdasarkan modal terakhir)
M₀, M₁, M₂, .........., M_n
M₁ = M₀ + P/100 . M₀ = (1 + P/100) M₀
M₂ = (1+P/100) M₀ + P/100 (1 + P/100) M₀ = (1 + P/100)(1+P/100)M₀
     = (1 + P/100)² M₀.
.
.
Mn = {1 + P/100}ⁿ M₀
Keterangan :
M₀ = Modal awal
M_n = Modal setelah n periode
p   = Persen per periode atau suku bunga
n   = Banyaknya periode
Catatan:
Rumus bunga majemuk dapat juga dipakai untuk masalah pertumbuhan tanaman, perkembangan bakteri (p > 0) dan juga untuk masalah penyusutan mesin, peluruhan bahan radio aktif (p < 0).

Rabu, 27 November 2013

Pemuaian

PEMUAIAN

Pengertian Pemuaian
Pemuaian adalah bertambahnya ukuran suatu benda karena pengaruh perubahan suhu atau bertambahnya ukuran suatu benda karena menerima kalor.
Pemuaian terjadi pada 3 zat yaitu pemuaian pada zat padat, pada zat cair, dan pada zat gas.
Pemuaian pada zat padat ada 3 jenis yaitu pemuaian panjang (untuk satu demensi), pemuaian luas (dua dimensi) dan pemuaian volume (untuk tiga dimensi). Sedangkan pada zat cair dan zat gas hanya terjadi pemuaian volume saja, khusus pada zat gas biasanya diambil nilai koofisien muai volumenya sama dengan 1/273.
Pemuaian panjang
adalah bertambahnya ukuran panjang suatu benda karena menerima kalor. Pada pemuaian panjang nilai lebar dan tebal sangat kecil dibandingkan dengan nilai panjang benda tersebut. Sehingga lebar dan tebal dianggap tidak ada. Contoh benda yang hanya mengalami pemuaian panjang saja adalah kawat kecil yang panjang sekali.
Pemuaian panjang suatu benda dipengaruhi oleh beberapa faktor yaitu panjang awal benda, koefisien muai panjang dan besar perubahan suhu. Koefisien muai panjang suatu benda sendiri dipengaruhi oleh jenis benda atau jenis bahan.
Secara matematis persamaan yang digunakan untuk menentukan pertambahan panjang benda setelah dipanaskan pada suhu tertentu adalah

Bila ingin menentukan panjang akhir setelah pemanasan maka digunakan persamaan sebagai berikut :

Yang perlu diperhatikan adalah didala rumus tersebut banyak sekali menggunakan lambang sehingga menyulitkan dalam menghapal. Disarankan untuk sering menggunakan rumus tersebut dalam mengerjakan soal dan tidak perlu dihapal.
Pemuaian luas
adalah pertambahan ukuran luas suatu benda karena menerima kalor. Pemuaian luas terjadi pada benda yang mempunyai ukuran panjang dan lebar, sedangkan tebalnya sangat kecil dan dianggap tidak ada. Contoh benda yang mempunyai pemuaian luas adalah lempeng besi yang lebar sekali dan tipis.
Seperti halnya pada pemuian luas faktor yang mempengaruhi pemuaian luas adalah luas awal, koefisien muai luas, dan perubahan suhu. Karena sebenarnya pemuaian luas itu merupakan pemuian panjang yang ditinjau dari dua dimensi maka koefisien muai luas besarnya sama dengan 2 kali koefisien muai panjang. Pada perguruan tinggi nanti akan dibahas bagaimana perumusan sehingga diperoleh bahwa koefisien muai luas sama dengan 2 kali koefisien muai panjang.
Untuk menentukan pertambahan luas dan volume akhir digunakan persamaan sebagai berikut :

Pemuaian volume
adalah pertambahan ukuran volume suatu benda karena menerima kalor. Pemuaian volume terjadi benda yang mempunyai ukuran panjang, lebar dan tebal. Contoh benda yang mempunyai pemuaian volume adalah kubus, air dan udara. Volume merupakan bentuk lain dari panjang dalam 3 dimensi karena itu untuk menentukan koefisien muai volume sama dengan 3 kali koefisien muai panjang. Sebagaimana yang telah dijelskan diatas bahwa khusus gas koefisien muai volumenya sama dengan 1/273
Persamaan yang digunakan untuk menentukan pertambahan volume dan volume akhir suatu benda tidak jauh beda pada perumusan sebelum. Hanya saja beda pada lambangnya saja. Perumusannya adalah

Transformator

Transformator

Prinsip Kerja Transformator

Komponen Transformator (trafo)

Transformator (trafo) adalah alat yang digunakan untuk menaikkan atau menurunkan tegangan bolak-balik (AC). Transformator terdiri dari 3 komponen pokok yaitu: kumparan pertama (primer) yang bertindak sebagai input, kumparan kedua (skunder) yang bertindak sebagai output, dan inti besi yang berfungsi untuk memperkuat medan magnet yang dihasilkan.

Bagian-Bagian Transformator

Contoh Transformator Lambang Transformator

Prinsip Kerja Transformator

Prinsip kerja dari sebuah transformator adalah sebagai berikut. Ketika Kumparan primer dihubungkan dengan sumber tegangan bolak-balik, perubahan arus listrik pada kumparan primer menimbulkan medan magnet yang berubah. Medan magnet yang berubah diperkuat oleh adanya inti besi dan dihantarkan inti besi ke kumparan sekunder, sehingga pada ujung-ujung kumparan sekunder akan timbul ggl induksi. Efek ini dinamakan induktansi timbal-balik (mutual inductance).

Pada skema transformator di samping, ketika arus listrik dari sumber tegangan yang mengalir pada kumparan primer berbalik arah (berubah polaritasnya) medan magnet yang dihasilkan akan berubah arah sehingga arus listrik yang dihasilkan pada kumparan sekunder akan berubah polaritasnya.

Hubungan antara tegangan primer, jumlah lilitan primer, tegangan sekunder, dan jumlah lilitan sekunder, dapat dinyatakan dalam persamaan:

Vp = tegangan primer (volt)
Vs = tegangan sekunder (volt)
Np = jumlah lilitan primer
Ns = jumlah lilitan sekunder
Simbol Transformator

Berdasarkan perbandingan antara jumlah lilitan primer dan jumlah lilitan skunder transformator ada dua jenis yaitu:

Transformator step up yaitu transformator yang mengubah tegangan bolak-balik rendah menjadi tinggi, transformator ini mempunyai jumlah lilitan kumparan sekunder lebih banyak daripada jumlah lilitan primer (Ns > Np).
Transformator step down yaitu transformator yang mengubah tegangan bolak-balik tinggi menjadi rendah, transformator ini mempunyai jumlah lilitan kumparan primer lebih banyak daripada jumlah lilitan sekunder (Np > Ns).

Pada transformator (trafo) besarnya tegangan yang dikeluarkan oleh kumparan sekunder adalah:

Sebanding dengan banyaknya lilitan sekunder (Vs ~ Ns).
Sebanding dengan besarnya tegangan primer ( VS ~ VP).
Berbanding terbalik dengan banyaknya lilitan primer,

Sehingga dapat dituliskan:

Penggunaan Transformator

Transformator (trafo) digunakan pada peralatan listrik terutama yang memerlukan perubahan atau penyesuaian besarnya tegangan bolak-balik. Misal radio memerlukan tegangan 12 volt padahal listrik dari PLN 220 volt, maka diperlukan transformator untuk mengubah tegangan listrik bolak-balik 220 volt menjadi tegangan listrik bolak-balik 12 volt. Contoh alat listrik yang memerlukan transformator adalah: TV, komputer, mesin foto kopi, gardu listrik dan sebagainya.

ARUS DAN TEGANGAN LISTIK

ARUS LISTRIK

Arus listrik adalah banyaknya muatan listrik yang disebabkan dari pergerakan elektron-elektron, mengalir melalui suatu titik dalam sirkuit listrik tiap satuan waktu. Arus listrik (I) yang mengalir melalui penghantar didefinisikan sebagai banyaknya muatan listrik
(Q) yang mengalir setiap satu satuan waktu (t).

I = Q/t

Secara matematis dapat dituliskan:
I = arus listrik (A)
Q = muatan listrik (C)
t = selang waktu

TEGANGAN LISTRIK

Sumber tegangan listrik yaitu peralatan yang dapat menghasilkan beda potensial listrik secara terus menerus. Beda potensial listrik diukur dalam satuan volt (V). Alat yang digunakan adalah volmeter.

Beda potensial adalah usaha yang digunakan untuk memindahkan satuan muatan listrik . hubungan antara energi listrik, muatan listrik dan beda potensial dapat dituliskan dalam persamaan:

V= W/ Q

V = Beda potensial listrik dalam volt (V)

W = energi listrik dalam joule (J)

Q = muatan listrik dalam coulomb (C).

Selasa, 26 November 2013

Hukum Ohm Dan Kirchoff

Hukum Ohm dan Hukum Kirchoff

Hukum Ohm
Aliran arus listrik dalam suatu rangkaian tidak berakhir pada alat listrik. tetapi melingkar kernbali ke sumber arus. Pada dasarnya alat listrik bersifat menghambat alus listrik. Hubungan antara arus listrik, tegangan, dan hambatan dapat diibaratkan seperti air yang mengalir pada suatu saluran. Orang yang pertama kali meneliti hubungan antara arus listrik, tegangan. dan hambatan adalah Georg Simon Ohm (1787-1854) seorang ahli fisika Jerman. Hubungan tersebut lebih dikenal dengan sebutan hukum Ohm.
Setiap arus yang mengalir melalui suatu penghantar selalu mengalami hambatan. Jika hambatan listrik dilambangkan dengan R. beda potensial V, dan kuat arus I, hubungan antara R, V, dan I secara matematis dapat ditulis:

Hukum Kirchoff
Arus listrik yang melalui suatu penghantar dapat kita pandang sebagai aliran air sungai. Jika sungai tidak bercabang, jumlah air di setiap tempat pada sungai tersebut sama. Demikian halnya dengan arus listrik.

Jumlah kuat arus yang masuk ke suatu titik percabangan sama dengan jumlah kuat arus yang keluar dari titik percabangan tersebut. Pernyataan itu sering dikenal sebagai hukum I Kirchhoff karena dikemukakan pertama kali oleh Kirchhoff. Maka diperoleh persamaan :
I _masuk = I _keluar